可视化

从SNE到t-SNE

t-SNE 算法对每个数据点近邻的分布进行建模，其中近邻是指相互靠近数据点的集合。在原始高维空间中，我们将高维空间建模为高斯分布，而在二维输出空间中，我们可以将其建模为 t 分布。该过程的目标是找到将高维空间映射到二维空间的变换，并且最小化所有点在这两个分布之间的差距。与高斯分布相比 t 分布有较长的尾部，这有助于数据点在二维空间中更均匀地分布。

Preparation

条件概率：

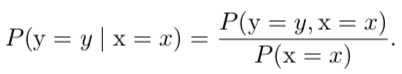
1. SNE

高维：

先把欧氏距离转化为条件概率。条件概率定义为$x_j$对于$x_i$的相似性。
假设一个高斯分布以$x_i$为中心，则条件概率：

即为在以$x_i$为中心的高斯分布下，若以邻域的概率密度成比例地选取邻域，$p_{j|i}$为$x_i$选择$x_j$作为近邻的概率。

这个条件概率分布函数是一个softmax函数，变量是点的相似度，这个相似度通过欧氏距离来定义。

设定 $p_{i|i} = 0$。

低维：

构建与高维相似的分布将计算条件概率 $q_{j|i}$ 中用到的高斯分布的方差设置为 1/2。

设定 $q_{i|i} = 0$。

目标：

让p、q的条件概率分布尽可能相似。通过最小化高低维分布之间的 KL散度。

通过梯度下降法进行迭代更新。

关于 KL散度 的进一步说明

KL散度具有不对称性，即在低维映射中不同的距离对应的惩罚权重是不同的。具体地，距离远的两点来表达距离近的两代男会产生很大的cost，而距离近的两点来表达距离远的两点则产生较小的cost，cost就是KL散度的结果C。

举个例子，假如高维中 $p_{j|i} = 0.8$，若在低维中用较小的 $q_{j|i} = 0.2$ 来表示它的话， $cost = 1.11$。反之，如果高维中，$p_{j|i} = 0.2$， 低维 $q_{j|i} = 0.8$, 则 $cost = -0.277$。

因此，SNE倾向于表达局部信息。

困惑度

困惑度与之前提到的高斯分布中的方差$\sigma_i$的确定有关。它是随 $\sigma_i$ 单调递增的。

条件概率矩阵 P 任意行的困惑度定义为：

其中 $H(P_i)$ 为 $P_i$ 的香农熵，即表达式如下：

困惑度的设置来确定高斯分布方差

在 SNE 和 t-SNE 中，困惑度是我们设置的参数（通常为 5 到 50 ）。困惑度随着熵增而变大，因此如果我们希望有更高的困惑度，那么所有的 $p_{j|i}$（对于给定的 i）就会彼此更相近一些。

为了达到相应的困惑度，我们就得利用困惑度与 $\sigma_i$ 单调递增的关系去进行二分查找，然后确定一个最优的 $\sigma_i$，从而达到我们要设置的困惑度值。于是$\sigma_i$就通过这个过程被确定下来了。

2. 对称SNE

SNE的条件概率对于 $p_{j|i}$ 和 $p_{i|j}$ 是不对称的，它的梯度实现起来比较困难。对称SNE是为了解决SNE梯度实现困难的问题。对称SNE使用了联合概率分布，取缔了条件概率分布。

高维

定义新的联合概率分布 $p_{ij}$ 是原来的条件概率分布 $p_{j|i}$ 和 $p_{i|j}$ 两项的均值。这样实现了$p_{ij} = p_{ji}$。

低维

低维中同样变成了联合概率分布，具体做法：把SNE中的分母做了改动，现在分母中的求和是对整个矩阵进行的。

优化求解

对称SNE 最小化 $p_{ij}$ 和 $q_{ij}$ 的联合概率分布与 $p_{i|j}$ 和 $q_{i|j}$ 的条件概率之间的 KL 散度。

对称SNE的梯度变简单了。

3. t-SNE

t-SNE使用了对称SNE，高维空间是之前的高斯分布，低维空间采用了t分布。

假设 $q_{ij}$ 服从自由度为1的 t分布，t-分布是一个长尾分布。

• t分布相对高斯分布比较矮宽，t分布让高维空间中中低距离在映射后能有一个较大的距离。
• t分布尾部更高，受异常值的影响更小。
• t分布自由度越大，越接近高斯分布。

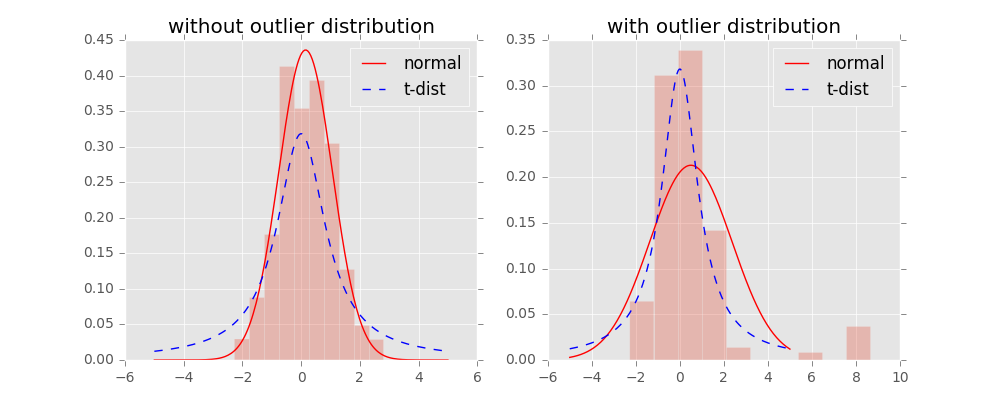
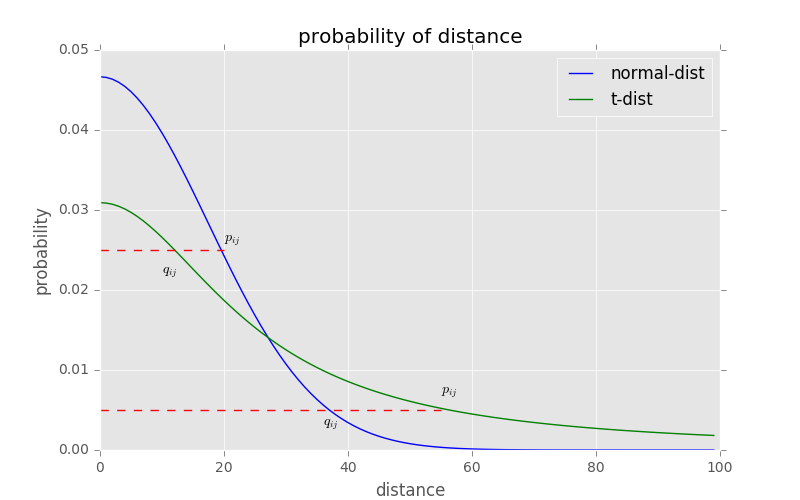
如上图所示，是高斯分布与t分布的对比。横轴表示点之间距离，纵轴表示相似度（联合概率）。t分布代表低维空间，高斯分布代表高维空间。

t分布实现了簇内聚集，簇间疏远的特点：

• 对于相似度大的点，t分布在低维空间的距离更小；
• 对于相似对小的点，t分布在低维空间中的距离更大；

低维空间的t分布定义

使用自由度为1的t分布来重新定义 $q_{ij}$.

$q_{ij}=\frac{ (1 + \left | y_i-y_j \right |^2)^{-1}}{\sum_{k \neq l} (1 + \left | y_k-y_l \right |^2)^{-1}}$

梯度变为：

$\frac{\delta C}{\delta y_i}=4\sum_{j}(p_{ij}-q_{ij})(y_i-y_j)(1 + \left | y_i-y_j \right |^2)^{-1}$

拥挤问题

当我们试图将一个高维数据集表征为 2 或 3 个维度时，很难将邻近的数据点与中等距离的数据点区分开来，因为这些数据点都聚集在一块区域。再比如，假如一个三维球体内部均匀分布了很多点，如果想把所有点直接投影到同一个二维平面上，那会有很多点是重合的。

t-分布用来解决拥挤问题的思路：假如我们想把之前球体内的所有点的信息尽可能都表达出来，可以把由于投影所重合的点用不同的距离表示，其中距离的差别很小，这样原来在那些距离上的点会被赶到更远的地方。

t分布的长尾特性意味着：距离更远的点依然能给和高斯分布下距离小的点相同的概率值，从而达到高、低维空间对应点概率相同的目的。

References

[1]详解可视化利器 t-SNE 算法：数无形时少直觉

[2]t-SNE完整笔记

[3]t-SNE分析的原理

[4]从SNE到t-SNE再到LargeVis